SISTEMA GRACELI ESTADO-DIMENSIONAL-CATEGORIAL [COM MAIS DE DUZENTAS DIMENSÕES]
SISTEMA DE MAIS DE DUZENTAS DIMENSÕES NO SDCTIE GRACELI
TERCEIRA QUANTIZAÇÃO PELO SDCTIE GRACELI
TRANS-QUÂNTICA SDCTIE GRACELI, TRANSCENDENTE, RELATIVISTA SDCTIE GRACELI, E TRANS-INDETERMINADA.
FUNDAMENTA-SE EM QUE TODA FORMA DE REALIDADE SE ENCONTRA EM TRANSFORMAÇÕES, INTERAÇÕES, TRANSIÇÕES DE ESTADOS [ESTADOS DE GRACELI], ENERGIAS E FENÔMENOS DENTRO DE UM SISTEMA DE DEZ OU MAIS DIMENSÕES DE GRACELI, E CATEGORIAS DE GRACELI.
FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI
FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS =
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.
x [EQUAÇÃO DE DIRAC].
+ FUNÇÃO TÉRMICA.
+ FUNÇÃO DE RADIOATIVIDADE
, + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ ENTROPIA REVERSÍVEL
+ FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
ENERGIA DE PLANCK
X
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG
XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
x
sistema de dez dimensões de Graceli + DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..
- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.
xsistema de transições de estados, e estados de Graceli, ESTADOS DE GRACELI TÉRMICOS E ESTADOS DOS ELEMENTOS QUÍMICO [ESTADOS ESPECÍFICOS DA MATÉRIA E ESTRUTURAS DE ELEMENTOS QUÍMICOS] [ONDE OS ESTADOS DOS ELEMENTOS QUÍMICO, MOLÉCULAS, ESTRUTURA ELETRÔNICA E MOLECULAR, E SUA TOPOGEOMETRIA DIMENSIONAL PASSAM A SEREM DIMENSÕES REPRESENTANDO ESTRUTURAS, ENERGIAS, INTERAÇÕES, TRANSFORMAÇÕES, FENÔMENOS, E OUTROS, LEVANDO AS DIMENSÕES PARA MAIS DE DUZENTAS]. fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.
+ FUNÇÃO TÉRMICA.
+ FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
xsistema de dez dimensões de Graceli +DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.xsistema de transições de estados, e estados de Graceli, ESTADOS DE GRACELI TÉRMICOS E ESTADOS DOS ELEMENTOS QUÍMICO [ESTADOS ESPECÍFICOS DA MATÉRIA E ESTRUTURAS DE ELEMENTOS QUÍMICOS] [ONDE OS ESTADOS DOS ELEMENTOS QUÍMICO, MOLÉCULAS, ESTRUTURA ELETRÔNICA E MOLECULAR, E SUA TOPOGEOMETRIA DIMENSIONAL PASSAM A SEREM DIMENSÕES REPRESENTANDO ESTRUTURAS, ENERGIAS, INTERAÇÕES, TRANSFORMAÇÕES, FENÔMENOS, E OUTROS, LEVANDO AS DIMENSÕES PARA MAIS DE DUZENTAS].fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].
número atômico, estrutura eletrônica, níveis de energia - TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI.
- X
- CATEGORIAS DE GRACELI
- T l T l E l Fl dfG l
X [ESTADO QUÂNTICO].
ONDE ESTADOS QUÍMICO, ESTADOS E NÍVEIS DE ENERGIA, MOLÉCULAS E OUTROS PASSAM A SEREM DIMENSÕES, FORMANDO ASSIM, UM SISTEMA DE MAIS DE DUZENTAS DIMENSÕES.
E CATEGORIAS FÍSICO-QUÍMICA DE GRACELI. QUE SÃO.
TIPOS DE ESTRUTURAS, ENERGIAS, FENÔMENOS, E OUTROS.
INTENSIDADE OU NÍVEIS DE TRANSFORMAÇÕES,
POTENCIAL DE INTERAGIR, DE TRANSFORMAR, E OUTROS.
E TEMPO DE AÇAO, ONDE OS FENÔMENOS NÃO OBEDECEM UMA HOMOGENEIDADE NOS PROCESSOS, DO INÍCIO AO FIM.
VEJAMOS PARA NÍVEIS DE ENERGIA NO ÁTOMO.
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI.
- X
- CATEGORIAS DE GRACELI
- T l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLl * D
Nível de energia
.
onde c, velocidade da luz, é igual a .[3]
x
Na teoria quântica de campos, as distribuições de Wightman podem ser analiticamente continua a funções analíticas em espaço euclidiano com o domínio restrito ao conjunto ordenado de pontos no espaço euclidiano sem pontos coincidentes. Essas funções são chamadas as funções Schwinger, em homenagem a Julian Schwinger. São funções analíticas, simétricas sob a permutação de argumentos[1] (antisimétrico para campos fermiônicos[2][3]) euclidianos covariante e satisfazem uma propriedade conhecida como positividade de reflexão.
Escolha qualquer coordenada arbitrária τ e escolha uma função de teste fN em um conjunto com N pontos como seus argumentos. Suponha que fN tem o seu apoio no subconjunto de tempo-ordenado de N pontos com 0 < τ1 < ... < τN. Selecione uma fN tal que para cada N positivo, com os f sendo zero para todos os N maiores do que algum número inteiro M. Dado um ponto x, seja o ponto refletido acerca do hiperplano τ = 0. Então,
onde * representa a conjugação complexa.[4]
O teorema de Osterwalder-Schrader afirma que as funções Schwinger que satisfazem essas propriedades podem ser analiticamente continuas dentro de uma teoria quântica de campos.[5] A integração de funcionais euclidianas satisfaz formalmente a reflexão de positividade[6][7]. Escolha qualquer polinômio funcional F do campo φ, que não depende do valor de φ(x) para os pontos x cujas coordenadas τ são não positivas. Então,
Uma vez que a ação S é real e pode ser dividida em S+, que só depende de φ no semi-espaço positivo[8] e S− que só depende de φ no semi-espaço negativo[9] e se S também acontece ser invariante sob a ação combinada de tomada de uma reflexão e conjugando complexo todos os campos; então, a quantidade precedente tem de ser não negativa.[10].
Função de onda na mecânica quântica é algo que descreve o estado quântico de um sistema de uma ou mais partículas, e contém todas as informações sobre o sistema considerado isolado. Quantidades associadas com os cálculos, tais como o momento médio de uma partícula, são derivados a partir da função de onda por meio de operações matemáticas que descrevem a sua interação com os dispositivos de observação. Assim, a função de onda é uma entidade central na mecânica quântica. Os símbolos mais comuns para uma função de onda são as letras gregas ψ ou Ψ . A equação de Schrödinger determina como a função de onda evolui ao longo do tempo, ou seja, a função de onda é a solução da equação de Schrödinger. A função de onda se comporta qualitativamente como outras ondas, como ondas de água ou ondas em uma corda, porque a equação de Schrödinger é matematicamente um tipo de equação de onda. Isso explica o nome "função de onda", e dá origem a dualidade onda-partícula. A onda da função de onda, no entanto, não é uma onda no espaço físico; é uma onda em um "espaço" matemático abstrato, que pode ser representado como "espaço de configuração", ou pode ser representado como "espaço de momentum", e, por isso se difere fundamentalmente de ondas de água ou ondas em uma corda.[1][2][3][4][5][6][7]
Uma função de onda para um determinado sistema não tem uma representação única. Mais comumente, é tomada como sendo uma função de todas as coordenadas de posição das partículas e do tempo, ou seja, a função de onda está na "posição espacial". No entanto, também pode considerar em vez uma função de onda no "espaço de momento"; uma função de todos os momentos das partículas e do tempo . Em geral, a função de onda de um sistema é uma função de variáveis contínuas e descontínuas que caracteriza o grau de liberdade do sistema, e há uma função de onda para todo o sistema, e não uma função de onda para cada partícula individual em certo sistema. Partículas elementares, como os elétrons, têm spin, e a função de onda deve incluir essa propriedade fundamental como um grau de liberdade intrínseca. A função de onda é espinoriail para os férmions, ou seja, para partículas com spin semi-inteiro (1/2, 3/2, 5/2, ...), ou tensorial para os bósons, que são partículas com spin inteiro (0, 1, 2, 3 , ...).
Na maioria dos tratamentos da mecânica quântica, a função de onda é um valor complexo. Em uma interpretação importante da mecânica quântica chamada a interpretação de Copenhague, o módulo de elasticidade ao quadrado da função de onda, |ψ|2 , é um número real se interpretado como a densidade de probabilidade de encontrar uma partícula em um dado local num determinado momento, se a posição da partícula está a ser medida. Uma vez que a função de onda é um valor complexo, apenas a sua fase relativa e a sua relativa magnitude podem ser medidas. Isso não diz nada diretamente sobre as magnitudes ou as direções das observações mensuráveis, tem de se aplicar operadores quânticos para a função de onda ψ e encontrar os seus próprios valores, que correspondem a conjuntos de possíveis resultados de medição.
No entanto, os números complexos não são necessariamente usados em todos os cálculos. Louis de Broglie em seus últimos anos propôs uma função de onda de valor real ligada a uma função de onda complexa por uma constante de proporcionalidade e desenvolveu a teoria de Broglie-Bohm.
.
onde c, velocidade da luz, é igual a .[3]
x
Na teoria quântica de campos, as distribuições de Wightman podem ser analiticamente continua a funções analíticas em espaço euclidiano com o domínio restrito ao conjunto ordenado de pontos no espaço euclidiano sem pontos coincidentes. Essas funções são chamadas as funções Schwinger, em homenagem a Julian Schwinger. São funções analíticas, simétricas sob a permutação de argumentos[1] (antisimétrico para campos fermiônicos[2][3]) euclidianos covariante e satisfazem uma propriedade conhecida como positividade de reflexão.
Escolha qualquer coordenada arbitrária τ e escolha uma função de teste fN em um conjunto com N pontos como seus argumentos. Suponha que fN tem o seu apoio no subconjunto de tempo-ordenado de N pontos com 0 < τ1 < ... < τN. Selecione uma fN tal que para cada N positivo, com os f sendo zero para todos os N maiores do que algum número inteiro M. Dado um ponto x, seja o ponto refletido acerca do hiperplano τ = 0. Então,
onde * representa a conjugação complexa.[4]
O teorema de Osterwalder-Schrader afirma que as funções Schwinger que satisfazem essas propriedades podem ser analiticamente continuas dentro de uma teoria quântica de campos.[5] A integração de funcionais euclidianas satisfaz formalmente a reflexão de positividade[6][7]. Escolha qualquer polinômio funcional F do campo φ, que não depende do valor de φ(x) para os pontos x cujas coordenadas τ são não positivas. Então,
Uma vez que a ação S é real e pode ser dividida em S+, que só depende de φ no semi-espaço positivo[8] e S− que só depende de φ no semi-espaço negativo[9] e se S também acontece ser invariante sob a ação combinada de tomada de uma reflexão e conjugando complexo todos os campos; então, a quantidade precedente tem de ser não negativa.[10].
Função de onda na mecânica quântica é algo que descreve o estado quântico de um sistema de uma ou mais partículas, e contém todas as informações sobre o sistema considerado isolado. Quantidades associadas com os cálculos, tais como o momento médio de uma partícula, são derivados a partir da função de onda por meio de operações matemáticas que descrevem a sua interação com os dispositivos de observação. Assim, a função de onda é uma entidade central na mecânica quântica. Os símbolos mais comuns para uma função de onda são as letras gregas ψ ou Ψ . A equação de Schrödinger determina como a função de onda evolui ao longo do tempo, ou seja, a função de onda é a solução da equação de Schrödinger. A função de onda se comporta qualitativamente como outras ondas, como ondas de água ou ondas em uma corda, porque a equação de Schrödinger é matematicamente um tipo de equação de onda. Isso explica o nome "função de onda", e dá origem a dualidade onda-partícula. A onda da função de onda, no entanto, não é uma onda no espaço físico; é uma onda em um "espaço" matemático abstrato, que pode ser representado como "espaço de configuração", ou pode ser representado como "espaço de momentum", e, por isso se difere fundamentalmente de ondas de água ou ondas em uma corda.[1][2][3][4][5][6][7]
Uma função de onda para um determinado sistema não tem uma representação única. Mais comumente, é tomada como sendo uma função de todas as coordenadas de posição das partículas e do tempo, ou seja, a função de onda está na "posição espacial". No entanto, também pode considerar em vez uma função de onda no "espaço de momento"; uma função de todos os momentos das partículas e do tempo . Em geral, a função de onda de um sistema é uma função de variáveis contínuas e descontínuas que caracteriza o grau de liberdade do sistema, e há uma função de onda para todo o sistema, e não uma função de onda para cada partícula individual em certo sistema. Partículas elementares, como os elétrons, têm spin, e a função de onda deve incluir essa propriedade fundamental como um grau de liberdade intrínseca. A função de onda é espinoriail para os férmions, ou seja, para partículas com spin semi-inteiro (1/2, 3/2, 5/2, ...), ou tensorial para os bósons, que são partículas com spin inteiro (0, 1, 2, 3 , ...).
Na maioria dos tratamentos da mecânica quântica, a função de onda é um valor complexo. Em uma interpretação importante da mecânica quântica chamada a interpretação de Copenhague, o módulo de elasticidade ao quadrado da função de onda, |ψ|2 , é um número real se interpretado como a densidade de probabilidade de encontrar uma partícula em um dado local num determinado momento, se a posição da partícula está a ser medida. Uma vez que a função de onda é um valor complexo, apenas a sua fase relativa e a sua relativa magnitude podem ser medidas. Isso não diz nada diretamente sobre as magnitudes ou as direções das observações mensuráveis, tem de se aplicar operadores quânticos para a função de onda ψ e encontrar os seus próprios valores, que correspondem a conjuntos de possíveis resultados de medição.
No entanto, os números complexos não são necessariamente usados em todos os cálculos. Louis de Broglie em seus últimos anos propôs uma função de onda de valor real ligada a uma função de onda complexa por uma constante de proporcionalidade e desenvolveu a teoria de Broglie-Bohm.
Índice
Problemas de nomenclatura
O termo função de onda segundo a mecânica quântica tem um significado bastante diferente dependendo do contexto, seja na física clássica, seja no eletromagnetismo clássico.
Por causa da relação concreta entre função de onda e localização de uma partícula num espaço de posições, que se deriva da aproximação sucedida das Ondas de matéria, de Louis de Broglie, e demostrada no Experimento de Davisson-Germer, muitos textos sobre mecânica quântica têm um enfoque "ondulatório". O termo "função de onda" é usado para o vetor de estado por este ser a solução de uma equação de onda, a equação de Schrödinger.
Na química, especialmente, um dos objetivos da função de onda de elétrons é descrever os chamados orbitais eletrônicos; com isso, aumenta ainda mais a confusão de termos que se referem a um mesmo conceito.
O termo função de onda segundo a mecânica quântica tem um significado bastante diferente dependendo do contexto, seja na física clássica, seja no eletromagnetismo clássico.
Por causa da relação concreta entre função de onda e localização de uma partícula num espaço de posições, que se deriva da aproximação sucedida das Ondas de matéria, de Louis de Broglie, e demostrada no Experimento de Davisson-Germer, muitos textos sobre mecânica quântica têm um enfoque "ondulatório". O termo "função de onda" é usado para o vetor de estado por este ser a solução de uma equação de onda, a equação de Schrödinger.
Na química, especialmente, um dos objetivos da função de onda de elétrons é descrever os chamados orbitais eletrônicos; com isso, aumenta ainda mais a confusão de termos que se referem a um mesmo conceito.
Definição
O uso moderno do termo função de onda é para qualquer vetor ou função que descreva o estado de um sistema físico pela expansão em termos de outros estados do mesmo sistema. Normalmente, uma função de onda é:
- um vetor complexo com finitos componentes:
- ,
- um vetor complexo com infinitos componentes:
- ,
- .
Em todos os casos, a função de onda provê uma descrição completa do sistema físico ao qual está associado. Porém, deve-se frisar que uma função de onda não é unicamente determinada pelo sistema ao qual está associada, já que muitas funções de onda diferentes podem descrever o mesmo cenário físico.
O uso moderno do termo função de onda é para qualquer vetor ou função que descreva o estado de um sistema físico pela expansão em termos de outros estados do mesmo sistema. Normalmente, uma função de onda é:
- um vetor complexo com finitos componentes:
- ,
- um vetor complexo com infinitos componentes:
- ,
- .
Em todos os casos, a função de onda provê uma descrição completa do sistema físico ao qual está associado. Porém, deve-se frisar que uma função de onda não é unicamente determinada pelo sistema ao qual está associada, já que muitas funções de onda diferentes podem descrever o mesmo cenário físico.
Interpretação
A interpretação física da função de onda depende do contexto. Veja alguns exemplos a seguir:
- Uma partícula em uma dimensão espacial
A função de onda espacial associada a uma partícula em uma dimensão é uma função complexa definida no conjunto dos números reais.
Interpretação estatística de Born
Na interpretação de Max Born, o quadrado da função de onda, , é interpretado como a densidade de probabilidade de encontrar a partícula na posição x em determinado tempo t [8], por isso, a probabilidade de a medição da posição da partícula dar um valor no intervalo é
- .
Isto leva à condição de normalização
- .
já que a medição da posição de uma partícula deve resultar em um número real.
Esse pensamento sendo associado com a Interpretação de Copenhague que foi feita pelo próprio Niels Bohr e Werner Heisenberg, define que não é possível determinar exatamente a posição da partícula, é possível somente determinar a probabilidade estatística, sendo assim, neste caso é entendida como um dado considerado inquestionável já que "Não faz sentido especular para além daquilo que pode ser medido".[9]
Notação Bra-ket é uma notação padrão para descrever estados quânticos na teoria da mecânica quântica. Ela também é utilizada para denotar vetores e funcional linear abstratos na matemática pura. É assim chamada por ser o produto interno de dois estados denotados por um bracket, consistindo de uma parte esquerda, denominada bra, e uma parte direita, denominada ket. A notação foi criada por Paul Dirac, e por isso é também conhecida como notação de Dirac.[1][2]
A interpretação física da função de onda depende do contexto. Veja alguns exemplos a seguir:
- Uma partícula em uma dimensão espacial
A função de onda espacial associada a uma partícula em uma dimensão é uma função complexa definida no conjunto dos números reais.
Interpretação estatística de Born
Na interpretação de Max Born, o quadrado da função de onda, , é interpretado como a densidade de probabilidade de encontrar a partícula na posição x em determinado tempo t [8], por isso, a probabilidade de a medição da posição da partícula dar um valor no intervalo é
- .
Isto leva à condição de normalização
- .
já que a medição da posição de uma partícula deve resultar em um número real.
Esse pensamento sendo associado com a Interpretação de Copenhague que foi feita pelo próprio Niels Bohr e Werner Heisenberg, define que não é possível determinar exatamente a posição da partícula, é possível somente determinar a probabilidade estatística, sendo assim, neste caso é entendida como um dado considerado inquestionável já que "Não faz sentido especular para além daquilo que pode ser medido".[9]
Notação Bra-ket é uma notação padrão para descrever estados quânticos na teoria da mecânica quântica. Ela também é utilizada para denotar vetores e funcional linear abstratos na matemática pura. É assim chamada por ser o produto interno de dois estados denotados por um bracket, consistindo de uma parte esquerda, denominada bra, e uma parte direita, denominada ket. A notação foi criada por Paul Dirac, e por isso é também conhecida como notação de Dirac.[1][2]
Índice
Bras e kets
Uso mais comum: Mecânica quântica
Em mecânica quântica, o estado físico de um sistema é identificado como um raio unitário em um espaço de Hilbert separável complexo, ou, equivalentemente, por um ponto no espaço de Hilbert projetado de um sistema. Cada vetor no raio é chamado um "ket" e escrito como que deve ser lido como "psi ket".[3]
O ket pode ser visualizado como um vetor coluna e (dada uma base para o espaço de Hilbert) escrito por extenso em componentes,
quando o espaço de Hilbert considerado possuir finitas dimensões. Em espaços de dimensão infinita, há infinitas componentes e o ket deve ser escrito em notação de função, precedido por um bra (veja abaixo). Por exemplo,
Todo ket possui um bra dual, escrito como Por exemplo, o bra correspondente ao acima deve ser um vetor linha
Isto é um funcional linear contínuo de para os números complexos definido por:
para todo ket
onde denota o produto interno definido sobre o espaço de Hilbert.Aqui, uma vantagem da notação bra-ket torna-se clara: quando removemos os parênteses (como é comum em funcionais lineares) e fundimos junto com as barra, obtemos que é a notação comum para produto interno no espaço de Hilbert. Esta combinação de um bra com um ket para formar um número complexo é chamada bra-ket ou bracket.
Em mecânica quântica a expressão (matematicamente o coeficiente para a projeção de em ) é tipicamente interpretada como a amplitude de probabilidade para o estado para o colapso no estado [4][5][6][7]
Os números quânticos descrevem valores de quantidades conservadas na dinâmica de um sistema quântico. No caso dos elétrons, os números quânticos podem ser definidos como "os conjuntos de valores numéricos que dão soluções aceitáveis para a equação de onda de Schrödinger para o átomo de hidrogênio",[1] e são de enorme relevância quando se trata de descrever a posição dos elétrons nos átomos.[2]
Em mecânica quântica, o estado físico de um sistema é identificado como um raio unitário em um espaço de Hilbert separável complexo, ou, equivalentemente, por um ponto no espaço de Hilbert projetado de um sistema. Cada vetor no raio é chamado um "ket" e escrito como que deve ser lido como "psi ket".[3]
O ket pode ser visualizado como um vetor coluna e (dada uma base para o espaço de Hilbert) escrito por extenso em componentes,
quando o espaço de Hilbert considerado possuir finitas dimensões. Em espaços de dimensão infinita, há infinitas componentes e o ket deve ser escrito em notação de função, precedido por um bra (veja abaixo). Por exemplo,
Todo ket possui um bra dual, escrito como Por exemplo, o bra correspondente ao acima deve ser um vetor linha
Isto é um funcional linear contínuo de para os números complexos definido por:
para todo ket
onde denota o produto interno definido sobre o espaço de Hilbert.Aqui, uma vantagem da notação bra-ket torna-se clara: quando removemos os parênteses (como é comum em funcionais lineares) e fundimos junto com as barra, obtemos que é a notação comum para produto interno no espaço de Hilbert. Esta combinação de um bra com um ket para formar um número complexo é chamada bra-ket ou bracket.
Em mecânica quântica a expressão (matematicamente o coeficiente para a projeção de em ) é tipicamente interpretada como a amplitude de probabilidade para o estado para o colapso no estado [4][5][6][7]
Os números quânticos descrevem valores de quantidades conservadas na dinâmica de um sistema quântico. No caso dos elétrons, os números quânticos podem ser definidos como "os conjuntos de valores numéricos que dão soluções aceitáveis para a equação de onda de Schrödinger para o átomo de hidrogênio",[1] e são de enorme relevância quando se trata de descrever a posição dos elétrons nos átomos.[2]
Índice
Introdução
Existem quatro números quânticos:
- número quântico principal;
- número quântico de momento angular ou azimutal (secundário);
- número quântico magnético;
- número quântico de spin.
Estes quatro números quânticos, além de se complementarem, nos permitem fazer uma descrição completa dos elétrons nos átomos, pois eles dizem o nível principal de energia do elétron, o subnível de energia, a orientação espacial da nuvem eletrônica e a orientação do próprio elétron na nuvem. Cada combinação dos quatro números quânticos é única para um elétron.
Os primeiros três números quânticos são usados para descrever orbitais atômicos e a caracterização dos elétrons que neles se encontram. O quarto número quântico, número quântico de spin é utilizado na descrição do comportamento específico de cada elétron. Assim, qualquer par de elétrons pode ter até três números quânticos iguais sendo que, neste caso, necessariamente, o quarto número quântico deverá ser diferente, ou seja, este par de elétrons estará ocupando o mesmo orbital sendo que os elétrons apresentam spins opostos.
Existem quatro números quânticos:
- número quântico principal;
- número quântico de momento angular ou azimutal (secundário);
- número quântico magnético;
- número quântico de spin.
Estes quatro números quânticos, além de se complementarem, nos permitem fazer uma descrição completa dos elétrons nos átomos, pois eles dizem o nível principal de energia do elétron, o subnível de energia, a orientação espacial da nuvem eletrônica e a orientação do próprio elétron na nuvem. Cada combinação dos quatro números quânticos é única para um elétron.
Os primeiros três números quânticos são usados para descrever orbitais atômicos e a caracterização dos elétrons que neles se encontram. O quarto número quântico, número quântico de spin é utilizado na descrição do comportamento específico de cada elétron. Assim, qualquer par de elétrons pode ter até três números quânticos iguais sendo que, neste caso, necessariamente, o quarto número quântico deverá ser diferente, ou seja, este par de elétrons estará ocupando o mesmo orbital sendo que os elétrons apresentam spins opostos.
Número quântico principal, n
O número quântico principal pode tomar como valor qualquer número inteiro positivo. Como o próprio nome o sugere, este número quântico é o mais importante, pois o seu valor define a energia do átomo de hidrogênio (e de outro átomo monoelectrónico de carga nuclear Z) por meio da equação:
onde m e e são a massa dos nêutrons e a carga do elétron, ε0 é a permissividade do vácuo, e h é a constante de Planck. Esta equação foi obtida como resultado da equação de Schrodinger e é desigual a uma das equações obtidas por Bohr, utilizando os seus postulados correctos.
O número quântico principal pode tomar como valor qualquer número inteiro positivo. Como o próprio nome o sugere, este número quântico é o mais importante, pois o seu valor define a energia do átomo de hidrogênio (e de outro átomo monoelectrónico de carga nuclear Z) por meio da equação:
onde m e e são a massa dos nêutrons e a carga do elétron, ε0 é a permissividade do vácuo, e h é a constante de Planck. Esta equação foi obtida como resultado da equação de Schrodinger e é desigual a uma das equações obtidas por Bohr, utilizando os seus postulados correctos.
Número quântico de momento angular, l
O número quântico de momento angular, ou azimutal, informa-nos sobre a forma dos orbitais. Como o próprio nome indica, o valor de l define o momento angular do elétron, sendo que o aumento do seu valor implica o aumento correspondente do valor do momento angular. Deste modo, a energia cinética do elétron é associada ao movimento angular e esta dependente da energia total do elétron, pelo que é natural que os valores permitidos de l estejam associados ao número quântico principal. Para um dado valor de n, l pode ter como valores possíveis os números inteiros de 0 a .
O número quântico de momento angular, ou azimutal, informa-nos sobre a forma dos orbitais. Como o próprio nome indica, o valor de l define o momento angular do elétron, sendo que o aumento do seu valor implica o aumento correspondente do valor do momento angular. Deste modo, a energia cinética do elétron é associada ao movimento angular e esta dependente da energia total do elétron, pelo que é natural que os valores permitidos de l estejam associados ao número quântico principal. Para um dado valor de n, l pode ter como valores possíveis os números inteiros de 0 a .
Número quântico magnético, ml
O número quântico magnético especifica a orientação permitida para uma nuvem eletrônica no espaço, sendo que o número de orientações permitidas está diretamente relacionado à forma da nuvem (designada pelo valor de l). Dessa forma, este número quântico pode assumir valores inteiros de -l, passando por zero, até +l.
- l = 0 : corresponde ao subnível s, onde existe somente uma orientação (ml = 0).
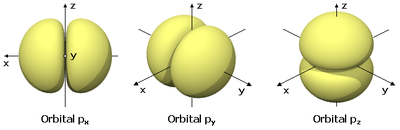
- l = 1 : corresponde ao subnível p, onde existem três orientações permitidas, que surgem em decorrência dos três valores de ml (+1, 0, -1). Os três orbitais p são denominados px, py e pz e são orientados de acordo com os três eixos cartesianoss (x, y e z).
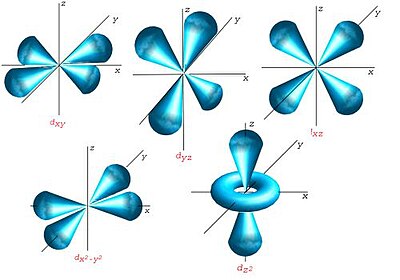
- l = 2 : corresponde ao subnível d onde existem cinco orientações permitidas, ou seja, cinco valores de ml (-2, -1, 0, +1, +2). São designados por dz² (orientação coincidente com o eixo z), dx²-y² (orientação coincidente com os eixos x e y, simultaneamente), dxy (orientado entre os eixos x e y), dyz (orientado entre os eixos y e z) e dxz (orientado entre os eixos x e z).
O número quântico magnético especifica a orientação permitida para uma nuvem eletrônica no espaço, sendo que o número de orientações permitidas está diretamente relacionado à forma da nuvem (designada pelo valor de l). Dessa forma, este número quântico pode assumir valores inteiros de -l, passando por zero, até +l.
- l = 0 : corresponde ao subnível s, onde existe somente uma orientação (ml = 0).
- l = 1 : corresponde ao subnível p, onde existem três orientações permitidas, que surgem em decorrência dos três valores de ml (+1, 0, -1). Os três orbitais p são denominados px, py e pz e são orientados de acordo com os três eixos cartesianoss (x, y e z).
- l = 2 : corresponde ao subnível d onde existem cinco orientações permitidas, ou seja, cinco valores de ml (-2, -1, 0, +1, +2). São designados por dz² (orientação coincidente com o eixo z), dx²-y² (orientação coincidente com os eixos x e y, simultaneamente), dxy (orientado entre os eixos x e y), dyz (orientado entre os eixos y e z) e dxz (orientado entre os eixos x e z).
Número quântico de spin, ms
O número quântico de spin são os autovalores possíveis do operador que indica a orientação da fonte extra de momento angular, sem analogia na mecânica clássica, relativa aos elétrons. Existem apenas dois valores possíveis para este número quântico, -1/2 e +1/2.
A tabela a seguir resume os significados de cada número quântico e os valores que eles podem assumir.
nome símbolo significado do orbital faixa de valores número quântico principal camada número quântico azimutal subnível número quântico magnético deslocamento de energia número quântico de spin spin
A tabela a seguir mostra a relação entre os números quânticos e os orbitais.
n l Orbital ml ms Número de Combinações 1 0 1s 0 -1/2, +1/2 2 2 0 2s 0 -1/2, +1/2 2 2 1 2p -1, 0, +1 -1/2, +1/2 6 3 0 3s 0 -1/2, +1/2 2 3 1 3p -1, 0, +1 -1/2, +1/2 6 3 2 3d -2, -1, 0, +1, +2 -1/2, +1/2 10 4 0 4s 0 -1/2, +1/2 2 4 1 4p -1, 0, +1 -1/2, +1/2 6 4 2 4d -2, -1, 0, +1, +2 -1/2, +1/2 10 4 3 4f -3, -2, -1, 0, +1, +2, +3 -1/2, +1/2 14
O número quântico de spin são os autovalores possíveis do operador que indica a orientação da fonte extra de momento angular, sem analogia na mecânica clássica, relativa aos elétrons. Existem apenas dois valores possíveis para este número quântico, -1/2 e +1/2.
A tabela a seguir resume os significados de cada número quântico e os valores que eles podem assumir.
| nome | símbolo | significado do orbital | faixa de valores |
|---|---|---|---|
| número quântico principal | camada | ||
| número quântico azimutal | subnível | ||
| número quântico magnético | deslocamento de energia | ||
| número quântico de spin | spin |
A tabela a seguir mostra a relação entre os números quânticos e os orbitais.
| n | l | Orbital | ml | ms | Número de Combinações |
|---|---|---|---|---|---|
| 1 | 0 | 1s | 0 | -1/2, +1/2 | 2 |
| 2 | 0 | 2s | 0 | -1/2, +1/2 | 2 |
| 2 | 1 | 2p | -1, 0, +1 | -1/2, +1/2 | 6 |
| 3 | 0 | 3s | 0 | -1/2, +1/2 | 2 |
| 3 | 1 | 3p | -1, 0, +1 | -1/2, +1/2 | 6 |
| 3 | 2 | 3d | -2, -1, 0, +1, +2 | -1/2, +1/2 | 10 |
| 4 | 0 | 4s | 0 | -1/2, +1/2 | 2 |
| 4 | 1 | 4p | -1, 0, +1 | -1/2, +1/2 | 6 |
| 4 | 2 | 4d | -2, -1, 0, +1, +2 | -1/2, +1/2 | 10 |
| 4 | 3 | 4f | -3, -2, -1, 0, +1, +2, +3 | -1/2, +1/2 | 14 |
De onde surgem os números quânticos?
Na teoria de Bohr era necessário postular a existência de números quânticos. Contudo, na mecânica quântica, estes números surgem naturalmente da solução matemática da equação de Schrödinger.
Equação de Schrödinger Dependente do Tempo (geral)
Na teoria de Bohr era necessário postular a existência de números quânticos. Contudo, na mecânica quântica, estes números surgem naturalmente da solução matemática da equação de Schrödinger.
| Equação de Schrödinger Dependente do Tempo (geral) |
 [EQUAÇÃO DE DIRAC].
[EQUAÇÃO DE DIRAC].
 + FUNÇÃO DE RADIOATIVIDADE
+ FUNÇÃO DE RADIOATIVIDADE
 + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ FUNÇÃO DE TUNELAMENTO QUÂNTICO. + ENTROPIA REVERSÍVEL
+ ENTROPIA REVERSÍVEL ![\sigma =q(n\mu _{n}+p\mu _{p})[\Omega .cm]^{{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53d1173dd9d9ec55715f1f4beb1ea5dcd4932bc8) FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA ENERGIA DE PLANCK
ENERGIA DE PLANCK

 [ESTADO QUÂNTICO].
[ESTADO QUÂNTICO].
![{\displaystyle \int {\mathcal {D}}\phi F[\phi (x)]F[\phi ({\bar {x}})]^{*}e^{-S[\phi ]}=\int {\mathcal {D}}\phi _{0}\int _{\phi _{+}(\tau =0)=\phi _{0}}{\mathcal {D}}\phi _{+}F[\phi _{+}]e^{-S_{+}[\phi _{+}]}\int _{\phi _{-}(\tau =0)=\phi _{0}}{\mathcal {D}}\phi _{-}F[{\bar {\phi }}_{-}]^{*}e^{-S_{-}[\phi _{-}]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2fd207dbf32725b261dbb75b91374ee1cffc71d)





![[a, b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)



































Comentários
Postar um comentário